Что означает и как выглядит дорожный знак тупик?

Подгруппа

Понятие подгруппы более сложное, чем понятие подмножества. Не любое подмножество группового множества может образовать подгруппу.

В группе и в её подгруппе действует одна и та же групповая операция. Значит, чтобы выделить подгруппу из группы, надо в групповом множестве выделить такое подмножеств, чтобы это подмножество с этой
операцией само образовывало самостоятельную группу.

Понятно, что раз в подгруппе действует та же самая групповая операция, то значит, в подгруппу всегда входит единичный элемент группы. Бывает, что в одной группе можно найти несколько подгрупп, но каждая
из этих подгрупп обязательно будет содержать единичный элемент группы.

У каждой группы, в общем случае, всегда есть две её тривиальных подгруппы. Это подгруппа с одним единичным элементом и подгруппа, которая совпадает с самой группой. Эти две подгруппы любой группы
называются несобственными или тривиальными подгруппами. Если группа состоит только из одного элемента, то у неё только одна несобственная подгруппа.

Все другие подгруппы называются собственными (нетривиальными) подгруппами. Бывают такие группы, которые содержат только тривиальные подгруппы. А бывают и такие, которые кроме тривиальных подгрупп
содержат еще и собственные подгруппы.

Группы, у которых есть только тривиальные подгруппы, называются простыми группами. Это по аналогии с простыми числами. Простые числа, это такие числа, которые имеют только два своих делителя: число 1 и
само себя.

Рассмотрим примеры групп, которые имеют собственные подгруппы.

Группа для множества комплексных чисел с операцией сложения имеет в качестве подгруппы группу вещественных чисел с операцией сложения. В свою очередь группа вещественных чисел с операцией сложения имеет
подгруппу в виде группы рациональных чисел. При этом группа рациональных чисел с операцией сложения является ещё и подгруппой комплексных чисел с операцией сложения. («Подгруппа моей подгруппы является
моей подгруппой.»)

У группы рациональных чисел по сложению есть еще одна подгруппа, это группа целых чисел по сложению. Таким образом, группа целых чисел со сложением является ещё и подгруппой таких групп, как группа
вещественных чисел и группа комплексных чисел.

А вот натуральные числа с операцией сложения уже не являются подгруппой группы целых чисел, так как множество натуральных чисел с операцией сложения не образуют группы. Операция сложения не является
групповой операцией для множества натуральных чисел, так как для такого сочетания множества и операции не выполняется третье свойство группы, о существовании обратных элементов. (А в России и в Германии
не выполняется ещё и второе свойство группы, так как в этих странах число 0 не считается натуральным числом.)

Если в какой-то группе есть две подгруппы, то их пересечение всегда тоже является подгруппой данной группы. А вот объединение этих подгрупп не всегда является подгруппой данной группы.

Классические задачи теории графов и их решения

Один из первых опубликованных примеров работ по теории графов и применения графов — работа о «задаче с
Кёнигсбергскими мостами» (1736 г.), автором которой является выдающийся математик 18-го века Леонард Эйлер.
В задаче даны река, острова, которые омываются этой рекой, и несколько мостов. Вопрос задачи:
возможно ли, выйдя из некоторого пункта, пройти каждый мост только по одному разу и вернуться в
начальный пункт? (рисунок ниже)

Задачу можно смоделировать следующим образом: к каждому участку суши прикрепляется
одна точка, а две точки соединяются линией тогда и только тогда, когда соответствующие участки суши
соединены мостом (рисунок ниже, соединительные линии начерчены пунктиром). Таким образом, построен граф.

Ответ Эйлера на вопрос задачи состоит в следующем. Если бы у этой задачи было
положительное решение, то в получившемся графе существовал бы замкнутый путь, проходящий по рёбрам и
содержащий каждое ребро только один раз. Если существует такой путь, то у каждой вершины должно быть
только чётное число рёбер. Но в получившемся графе есть вершины, у которых нечётное число рёбер.
Поэтому задача не имеет положительного решения.

По устоявшейся традиции эйлеровым графом называется граф, в котором можно обойти все
вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное
число рёбер. Задача средней трудности на эйлеровы графы — в материале «Основные виды графов».

В 1847 г. Кирхгоф разработал теорию деревьев для решения совместной системы линейных
алгебраических уравнений, позволяющую найти значение силы тока в каждом проводнике (дуге) и в каждом
контуре электрической цепи. Абстрагируясь от электрических схем и цепей, которые содержат сопротивления,
конденсаторы, индуктивности и т.д., он рассматривал соответствующие комбинаторные структуры, содержащие
только вершины и связи (рёбра или дуги), причём для связей не нужно учитывать, каким типам электрических
элементов они соответствуют. Таким образом, Кирхгоф заменил каждую электрическую цепь соответствующим
графом и показал, что для решения системы уравнений необязательно рассматривать в отдельности каждый
цикл графа электрической цепи.

Кэли в 1858 г., занимаясь чисто практическими задачами органической химии, открыл
важный класс графов, называемых деревьями. Он стремился перечислить изомеры насыщенных углеводородов,
с данным числом атомов углерода. Кэли прежде всего сформулировал задачу абстрактно: найти число
всех деревьев с p вершинами, каждое из которых имеет вершины со степенями 1 и 4. Ему не удалось
сразу решить эту задачу, и он стал изменять её формулировку таким образом, чтобы можно было решить
новую задачу о перечислении:

• корневых деревьев (в которых выделена одна из вершин);
• всех деревьев;
• деревьев, у которых степени вершин не превышают 4;
• деревьев, у которых степени вершин равны 1 и 4 (постановка задачи из химии).

Какие театры располагаются в этих зданиях?

Вопрос 11. В Москве во второй половине XIX — начале ХХ века было несколько мест, где ночами шла карточная игра: Английский, Охотничий, Немецкий и Купеческий клубы. Однажды в Купеческом клубе Михаил Морозов проиграл за ночь миллион рублей. До 1909 года клуб был на одной улице, после переехал на соседнюю. В обоих упомянутых зданиях сегодня располагаются театры.

Выбрать один правильный вариант из предложенных ответов:

• Театр Вахтангова и театр «Эрмитаж» (ул. Арбат, д. 26, и ул. Новый Арбат, д. 11)
• Московский академический Музыкальный театр К.С. Станиславского и В.И. Немировича-Данченко и Московский государственный театр «Ленком Марка Захарова» (ул. Большая Дмитровка, д. 17, и ул. Малая Дмитровка, д. 6)
• Российский академический молодежный театр и театр имени М.Н. Ермоловой (Театральная пл., д. 2, и Тверская ул., д. 5/6)
• Московский театр на Таганке и Московский театр русской драмы под руководством М. Щепенко (ул. Земляной Вал, д. 76/21, и ул. Земляной Вал, д. 64)

Кулответ поискал информацию в интернете:

По мнению Кулответа правильный вариант: Московский академический Музыкальный театр К.С. Станиславского и В.И. Немировича-Данченко и Московский государственный театр «Ленком Марка Захарова» (ул. Большая Дмитровка, д. 17, и ул. Малая Дмитровка, д. 6)

Мощность множества

Интуиция подсказывает, что термин характеризует размер множества, а именно количество его элементов. И интуиция нас не обманывает!

Мощность пустого множества равна нулю.

Мощность множества  равна шести.

Мощность множества букв русского алфавита  равна тридцати трём.

И вообще – мощность любого конечного множества равно количеству элементов данного множества.

…возможно, не все до конца понимают, что такое конечное множество – если начать пересчитывать элементы этого множества, то рано или поздно счёт завершится. Что называется, и китайцы когда-нибудь закончатся.

Само собой, множества можно сравнивать по мощности и их равенство в этом смысле называется равномощностью. Равномощность определяется следующим образом:

Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.

Множество  студентов равномощно множеству  тем рефератов, множество  букв русского алфавита равномощно любому множеству из 33 элементов и т.д. Заметьте, что именно любому множеству из 33 элементов – в данном случае имеет значение лишь их количество. Буквы русского алфавита можно сопоставить не только с множеством номеров 1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы.

Гораздо более интересно обстоят дела с бесконечными множествами. Бесконечности тоже бывают разными! …зелёными и красными Самые «маленькие» бесконечные множества – это счётные множества. Если совсем просто, элементы такого множества можно пронумеровать. Эталонный пример – это множество натуральных чисел . Да – оно бесконечно, однако у каждого его элемента в ПРИНЦИПЕ есть номер.

Примеров очень много. В частности, счётным является множество всех чётных натуральных чисел . Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы:
Взаимно-однозначное соответствие установлено, следовательно, множества равномощны и множество  счётно. Парадоксально, но с точки зрения мощности – чётных натуральных чисел столько же, сколько и натуральных!

Множество целых чисел тоже счётно. Его элементы можно занумеровать, например, так:

Более того, счётно и множество рациональных чисел . Поскольку числитель – это целое число (а их, как только что показано, можно пронумеровать), а знаменатель – натуральное число, то рано или поздно мы «доберёмся» до любой рациональной дроби  и присвоим ей номер.

А вот множество действительных чисел  уже несчётно, т.е. его элементы пронумеровать невозможно. Данный факт хоть и очевиден, однако строго доказывается в теории множеств. Мощность множества действительных чисел также называют континуумом, и по сравнению со счётными множествами это «более бесконечное» множество.

Поскольку между множеством  и числовой прямой существует взаимно-однозначное соответствие (см. выше), то множество точек числовой прямой тоже несчётно. И более того, что на километровом, что на миллиметровом отрезке – точек столько же! Классический пример: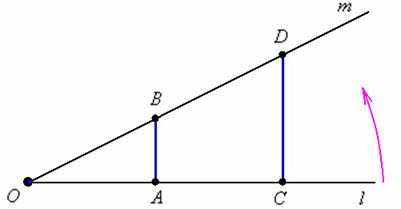
Поворачивая луч  против часовой стрелки до его совмещения с лучом  мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке  столько же точек, сколько и на отрезке и !

Данный парадокс, видимо, связан с загадкой бесконечности… но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди основы математической логики, а не философия =)

Спасибо за внимание и успехов вам в учёбе!

Решение заданий:

Задание 1

1)

2)  – это множество нечётных натуральных чисел:

3)

 – все точки  координатной плоскости
, удовлетворяющие двум указанным неравенствам. Аналогично:

Задание 2 Взаимно-однозначные функции на иллюстрациях урока Функции и графики:

(Переход на главную страницу)

Изоморфизм и гомоморфизм

Гомоморфизм

Одна группа гомоморфна другой группе, если любым двум элементам A и B из первой группы можно однозначно сопоставить два элемента A’ и B’, соответственно, из второй группы
так, что если AB=C, а A’B’=C’, то элементу C из первой группы однозначно сопоставляется элемент C’ из второй группы.

Фактически, это означает, что существует какая-то однозначная операция отображения всех элементов первой группы на все элементы второй группы так, что при этом сохраняются все отношения между элементами,
задаваемые групповыми операциями. Такое отображение называется гомоморфизмом.

Из этого понятно, что единичный элемент первой группы при гомоморфизме всегда соответствует единичному элементу второй группы. А все пары взаимно обратных элементов первой группы всегда соответствуют
парам взаимно обратных элементов второй группы.

Простой пример гомоморфизма. Группу целых четных чисел с операцией сложения можно однозначно отобразить на группу всех целых чисел с операцией умножения. При этом числу 0 первой группы
соответствует число 0 второй группы. Числу 2 первой группы соответствует число 1 второй группы. Числу 4 первой группы соответствует число 2 второй группы. И т.д. То же самое и с отрицательными числами. В
общем случае число n из второй группы является соответствием числа 2n из первой группы.

Гомоморфизм требует однозначности такого отображения, но не требует при этом взаимности этого отображения. То есть элемент A из первой группы имеет только один соответствующий ему элемент A’
из второй группы. Во второй группе нет никакого другого элемента, который соответствует элементу A из первой группы. Но вот для двух разных элементов A₁ и A₂ из
первой группы (A₁≠A₂) допускается иметь только один соответствующий им элемент A’ из второй группы.

В этом смысле вторая группа может не только иметь меньше элементов, чем первая группа, но и быть более простой, чем первая группа. Ядром гомоморфизма первой группы называется такая подгруппа первой
группы, которая при гомоморфизме переходит в единичный элемент второй группы.

Изоморфизм

Изоморфизм, это взаимно однозначный гомоморфизм.

То есть, когда элементу A первой группы не только соответствует один элемент A’ второй группы, но и элементу A’ соответствует только один элемент A из первой группы.

Если между двумя группами существует изоморфизм, то данные группы называются изоморфными. Изоморфные группы не отличаются друг от друга с точки зрения теории групп. С точки зрения теории групп изоморфные
группы являются совершенно одинаковыми. Элементы таких групп могут иметь разную математическую природу, операции таких групп также могут быть разными, но в теории групп, это одна и та же группа.

Рассмотрим пример изоморфизма. Пусть одна группа представляет собой 4 числа, 1, i, -1, -i, где i, это мнимая единица, а групповой операцией будет умножение этих чисел.
Данная группа изоморфна группе вращений плоскости, которые совмещают квадрат с самим собой при поворотах квадрата вокруг своего центра с групповой операцией последовательного применения двух вращений.

Соответствуют друг другу число 1 и поворот на 0 градусов, число i и поворот на 90 градусов, число (-1) и поворот на 180 градусов, число (-i) и поворот на 270 градусов. Можно
убедиться, что операция умножения в первой группе точно соответствует операции сочетания двух соответствующих поворотов из второй группы.

Изоморфизм в теории групп полезен тем, что позволяет перенести многие доказанные математиками вещи из одной области математики в другую, когда удается доказать изоморфизм основных групп в этих разных
областях математики.

2 вариант

1. Множество А «является разновидностью» множества В. Выберите аналогичное утверждение.

1) множество А равно множеству В
2) множество А — подмножество множества В
3) оба утверждения верны
4) все приведённые утверждения не верны

2. Выберите пример отношения «является разновидностью».

1) лошадь — домашнее животное
2) в классе две Даши и три Марины
3) оба утверждения верны
4) все приведённые утверждения не верны

3. Какие правила используют при составлении схемы разновидностей?

1) имя подмножества — рядом с именем множества
2) имя подмножества — ниже имени множества
3) имя множества и подмножества соединены стрелкой
4) специальных правил нет

4. Пусть объект В «является разновидностью» объекта А, и объект С «является разновидностью» объекта А. Является ли объект С разновидностью объекта В? Выберите верный ответ.

1) да, такое будет всегда
2) такое может быть, а может и не быть
3) нет, такого быть не может

5. Пусть объект А «является разновидностью» объекта В. У объекта А есть свойство 1. Можно ли утверждать, что объект В имеет свойство 1?

1) да
2) нет

6. Пусть объект А «является разновидностью» объекта В. У объекта В есть 5 свойств. Выберите верное утверждение.

1) у объекта А есть тоже 5 свойств, но других
2) у объекта А нет свойств иных, чем у объекта В
3) у объекта А есть такие же 5 свойств, как у В, и ещё дополнительные свойства, которых нет у В
4) у объекта А есть только некоторые из 5 свойств объекта В

7. Подумайте, может ли объект С являться разновидностью и множества А, и множества В, если А и В не пересекаются?

1) да
2) нет

8. Пусть множество А имеет 7 объектов, а множество В — 8 объектов. Какое минимальное число объектов может иметь объединение А и В?

1) 7
2) 8
3) 15
4) 1

Ответы на тест по информатике Отношение «является разновидностью» для 6 класса1 вариант
1-3
2-1
3-4
4-1
5-1
6-1
7-2
8-12 вариант
1-2
2-3
3-2
4-2
5-2
6-3
7-2
8-2

Отображение множеств

Отображение множества  во множество – это правило, по которому каждому элементу множества  ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой  – она ставит в соответствие каждому элементу  единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество  студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

 Векторы  Матрицы  Определители Комплексные числа (о, да!)  Теория пределов Что такое производная?

Установленное (добровольно или принудительно =)) правило  ставит в соответствие каждому студенту  множества  единственную тему реферата  множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества  образуют область определения функции (обозначается через ), а элементы множества  – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству  добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена –  одна из тем останется невостребованной.

Уважаемые студенты на 1-м ряду, не расстраивайтесь – остальные 20 человек после пар пойдут прибирать территорию университета от осенней листвы. Завхоз выдаст двадцать голиков, после чего будет установлено взаимно-однозначное соответствие между основной частью группы и мётлами…, а Вольдемар ещё и в магазин сбегать успеет =)

Теперь разберёмся со «школьной» функцией одной переменной. Пожалуйста, загляните на страницу Функции и графики (отроется на соседней вкладке), и в Примере 1 найдите график линейной функции .

Задумаемся, что это такое? Это правило , которое каждому элементу  области определения (в данном случае это все значения «икс») ставит в соответствие единственное значение . С теоретико-множественной точки зрения, здесь происходит отображение множества действительных чисел во множество действительных чисел:

Первое множество мы по-обывательски называем «иксами» (независимая переменная или аргумент), а второе – «игреками» (зависимая переменная или функция).

Далее взглянем на старую знакомую параболу  . Здесь правило  каждому значению «икс» ставит в соответствие его квадрат, и имеет место отображение:

Итак, что же такое функция одной переменной? Функция одной переменной  – это правило , которое каждому значению независимой переменной  из области определения ставит в соответствие одно и только одно значение .

Как уже отмечалось в примере со студентами, не всякая функция является взаимно-однозначной. Так, например, у функции  каждому «иксу» области определения  соответствует свой уникальный «игрек», и наоборот – по любому значению «игрек» мы сможем однозначно восстановить «икс». Таким образом, это биективная функция.

! На всякий случай ликвидирую возможное недопонимание: моя постоянная оговорка об области определения не случайна! Функция может быть определена далеко не при всех «икс», и, кроме того, может быть взаимно-однозначной и в этом случае. Типичный пример:  

А вот у квадратичной функции не наблюдается ничего подобного, во-первых: – то есть, различные значения «икс» отобразились в одно и то же значение «игрек»; и во-вторых: если кто-то вычислил значение функции и сообщил нам, что , то не понятно – этот «игрек» получен при  или при ? Что и говорить, взаимной однозначностью здесь даже не пахнет.

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

Определение графа

Строгое определение графа: графом G называется пара множеств непустое множество вершин а элементами множества Е являются некоторые двухэлементные подмножества Эти двухэлементные подмножества называются ребрами. Например,

Несложные графы изображают в виде графических схем, где вершины — точки, а ребра — соединяющие их линии. В этих схемах длина линий, их толщина и форма, а также взаиморасположение вершин не имеют никакого значения. Таким образом, граф — свободная конструкция, для которой имеет значение факт наличия связей между двумя вершинами и, в некоторых случаях, характер этих связей.

Если вершины принадлежат некоторому ребру то говорят, что это ребро инцидентно вершинам которые в свою очередь называются смежными. Если ребро инцидентно одной и той же вершине, то оно называется петлей. Вершина, не инцидентная никакому ребру, называется изолированной. Если в графе есть вершины, соединенные двумя или большим числом вершин, то такой граф называют мультиграфом (см. рис. 1.18).

Число ребер, инцидентных данной вершине, называется степенью (кратностью) данной вершины. В графе, изображенном на рис. 1.18, вершина имеет степень 6, т.к. ей инцидентны ребра а вершина имеет степень 5. Вершина имеет степень 0, т. е. это изолированная вершина. Граф без петель и кратных ребер называется простым или обыкновенным. Граф может быть задан и в виде квадратной таблицы — матрицы смежности графа.

Номера строк и столбцов этой матрицы совпадают с номерами вершин графа, а ее элемент есть число ребер, соединяющих вершины . Для графа, изображенного на рис. 1.18, матрица смежности имеет вид

Нумеровать вершины графа можно произвольным образом. Например, в графе, изображенном на рис. 1.18, перенумеруем вершины следующим образом: При этом матрица смежности изменится (сравните матрицы С и ).

Для графов существенно лишь число вершин и ребер, а также отношения инцидентности вершин и ребер. Следовательно, графы, отличающиеся только нумерацией вершин и сохраняющие отношения их инцидентности, отличаются лишь начертанием. Поэтому говорят, что матрица определяет графы с точностью до изоморфизма, а такие графы называются изоморфными. В подавляющем большинстве приложений изоморфные графы не различаются, и решения задач на изоморфных графах по существу совпадают. Граф называется планарным (плоским), если существует изоморфный ему граф, который может быть изображен на плоскости без пересечения ребер. На рис. 1.19 представлена пара изоморфных графов В первом из них ребра пересекаются, но поскольку в изоморфном ему графе ребра не пересекаются, то оба они являются планарными.

Ориентированным, или орграфом D, называется пара произвольное множество вершин и А — множество упорядоченных пар вершин, называемых дугами В паре первая вершина называется началом дуги, а вторая — концом дуги. На рисунках дуги изображаются стрелками (см. рис. 1.20).

Ориентированные графы задают в виде таблиц — матриц ин-циденций. Номера строк матрицы инциденций равны номерам вершин, а номера столбцов — номерам дуг. Если дуга выходит из вершины , то соответствующий элемент матрицы инциденций равен -1. Если же дуга входит в вершину то элемент равен +1. Все другие элементы столбца j равны нулю. Для ориентированного графа, изображенного на рис. 1.18, матрица инциденций имеет вид

Матрицы часто используются для задания графов в памяти компьютеров.

Граф называется частичным графом (суграфом) графа , если он содержит все вершины исходного графа и лишь часть ребер исходного графа, т.е. Подграфом графа называется граф, в который входит подмножество вершин исходного графа и все ребра, соединяющие вершины этого графа На рис. 1.21 представлены: подграф и частичный граф для данного исходного графа .

Что такое теория графов и что такое граф?

Теория графов — один из обширнейших разделов дискретной математики, широко применяется
в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических
цепей, коммуникации, психологии, психологии, социологии, лингвистике, других областях знаний. Теория графов систематически
и последовательно изучает свойства графов, о которых можно сказать, что они состоят из множеств точек и
множеств линий, отображающих связи между этими точками. Основателем теории графов считается Леонард
Эйлер (1707-1882), решивший в 1736 году известную в то время задачу о кёнигсбергских мостах.

Графы строят для того, чтобы отобразить отношения на множествах.
Пусть, например, множество —
множество людей, а каждый элемент будет отображён в виде точки

Множество —
множество связок (прямых, дуг, отрезков — пока не важно). На множестве A задано отношение
знакомства между людьми из этого множества

Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Естественно, число знакомых у одних людей может отличаться от числа знакомых у других людей, а некоторые
вполне могут и не быть ни с кем знакомы (такие элементы будут точками, не соединёнными ни с одной другой). Вот и получился граф!

То, что мы сначала назвали «точками», следует называть вершинами графа, а то, что
называли «связками» — рёбрами графа.

Теория графов не учитывает конкретную природу множеств A и B. Существует
большое количество самых разных конкретных задач, при решении которых можно временно забыть о специфическом
содержании множеств и их элементов

Эта специфика никак не сказывается на ходе решения задачи, независимо
от её трудности! Например, при решении вопроса о том, можно ли из точки a добраться до
точки e, двигаясь только по соединяющим точки линиям, неважно, имеем ли мы дело с людьми,
городами, числами и т.д. Но, когда задача решена, мы получаем решение, верное для любого содержания,
которое было смоделировано в виде графа

Не удивительно поэтому, что теория графов — один из самых
востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может
обсудить с собеседником и вопросы любви, и вопросы музыки или спорта, и вопросы решения различных задач,
причем делает это без всякого перехода (переключения), без которого в подобных случаях не обойтись человеку.

А теперь строгие математические определения графа.

Определение 1. Графом называется система объектов произвольной
природы (вершин) и связок (рёбер), соединяющих некоторые пары этих объектов.

Определение 2. Пусть – (непустое) множество вершин, элементы – вершины.
Граф с множеством вершин есть некоторое
cемейство пар вида: , где , указывающих,
какие вершины остаются соединёнными. Каждая пара — ребро графа.
Множество — множество рёбер графа. Вершины и – концевые точки ребра .

Графы как структура данных. Широким применением теории графов в
компьютерных науках и информационных технологиях обусловлено добавлением к вышеизложенным определениям
понятия графа как структуры данных. В компьютерных науках и информационных технологиях граф определяется
как нелинейная структура данных. Что же тогда — линейная структура данных и чем от них отличаются графы?
Линейные структуры данных характеризуются тем, что связывают элементы отношениями типа «простого соседства».
Линейными структурами данных являются, например, массивы, таблицы, списки, очереди, стеки, строки. В
противоположность им нелинейные структуры данных — такие, в которых элементы располагаются на различных
уровнях иерархии и подразделяются на три вида: исходные, порождённые и подобные. Итак, граф — нелинейная
структура данных.

Слово граф греческого происхождения, от слов «пишу», «описываю». Из начала этой статьи
известно, что именно описывает граф: описывает он отношения. То есть, любой граф описывает отношения. И
наоборот: любое отношение можно описать в виде графа.

Координатная прямая и числовые промежутки как объединение их частей

Отметим на координатной прямой произвольную точку, например, с координатой -5,4. Указанная точка разобьет координатную прямую на два числовых промежутка – два открытых луча (-∞, -5,4) и (-5,4, +∞) и собственно точку. Нетрудно увидеть, что в соответствии с определением объединения множеств любое действительное число будет принадлежать объединению (-∞, -5,4)∪ {-5,4} ∪(-5,4, +∞). Т.е. множество всех действительных чисел R = (-∞; +∞) возможно представить в виде полученного выше объединения. И наоборот, полученное объединение будет являться множеством всех действительных чисел.

Отметим, что заданную точку возможно присоединить к любому из открытых лучей, тогда он станет простым числовым лучом (-∞, -5,4 или -5,4, +∞). При этом множество R будет описываться следующими объединениями: (-∞, -5,4 ∪ (-5,4, +∞) или (-∞, -5,4) ∪ -5,4, +∞)..

Подобные рассуждения действительны не только относительно точки координатной прямой, но и относительно точки на любом числовом промежутке. Т.е., если мы возьмем любую внутреннюю точку любого произвольного промежутка, его возможно будет представить, как объединение его частей, полученных после деления заданной точкой, и самой точки. К примеру, задан полуинтервал (7, 32 и точка 13, принадлежащая этому числовому промежутку. Тогда заданный полуинтервал можно представить в виде объединения (7, 13) ∪ {13} ∪ (13, 32 и обратно. Мы можем включить число 13 в любой из промежутков и тогда заданное множество (7, 32 можно представить, как (7, 13 ∪ (13, 32 или (7, 13 ∪ (13, 32. Также мы можем взять в качестве исходных данных не внутреннюю точку заданного полуинтервала, а его конец (точку с координатой 32), тогда заданный полуинтервал можно представить, как объединение интервала (7, 32) и множества из одного элемента {32}. Таким образом: (7, 32 = (7, 32) ∪ {32}.

Еще один вариант: когда берется не одна, а несколько точек на координатной прямой или числовом промежутке. Эти точки разобьют координатную прямую или числовой промежуток на несколько числовых промежутков, а объединение этих промежутков будут составлять исходные множества. К примеру, на координатной прямой заданы точки с координатами -6, , 8, которые разобьют ее на промежутки: (-∞, -6), (-6,), (, 8), (8, +∞). При этом множество всех действительных чисел, олицетворением чего и является координатная прямая, возможно представить в виде объединения полученных промежутков и указанных чисел:

(-∞, -6) ∪ {-6} ∪(-6,) ∪ {} ∪ (,  ∪ {8} ∪ (8, +∞).